Rendering of Refraction at Transparent Polygonal Objects in Real-Time

The goal of this thesis was to render two-sided refraction at polygonal objects in real-time using OpenGL.

Description

In order to render refractive models in real-time, the algorithm described in [1] was implemented in C++, GLSL, and OpenGL. It can handle any OBJ file of triangles and quads. After calculating the first refraction when the eye ray hits the object, the algorithm in the fragment shader uses binary search over a precomputed depth map to approximate the second intersection point with the object. It then calculates the second refracted vector with which to index a dynamic environment map to get the desired colour.

Results

The program renders nearly any given model realistically as if it was transparent (e.g. made of glass). It is still capable of retaining a high performance. Many parameters can be adjusted in online. The following video shows an example:

The following plot shows the performance of the method for the bunny model.

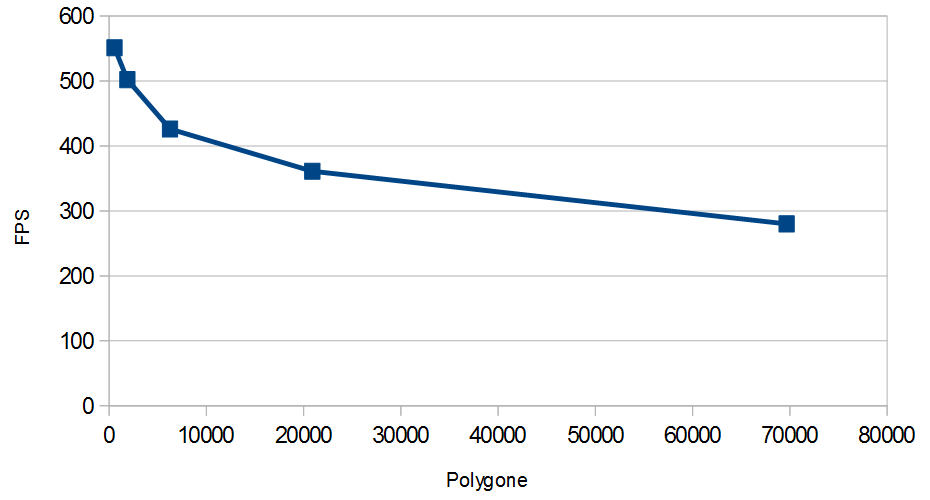The timings were done on a PC with Intel Core i7-4770K at 3.5 GHZ and an Nvidia Geforce GTX 780. The times or the shader-based redering include everything (rendering the dynamic environment map, the opaque geometry, and the transparent object, the latter of which includes several passes).

The following image shows a comparison of our shader-based refraction implementation, compared with the same scene rendered using raytracing (Blender). (Unfortunately, the viewpoints were not exactly the same.)

Both images were rendered at 800x800 pixels, and the refraction index was 1.5 . The raytraced image was rendered using 18 samples per pixel, with a maximal recursion depth of 10. In this scene, the shader-based renderer achieved 180 FPS, while the raytracer took 2 minutes 50 seconds.

Files

Full version of the thesis (German only, sorry)

References

[1] Li, Shuai; Gao, Yujian; Hao, Aimin; Wang, Lili: Interactive Two-sided Refraction for Dynamic Object on GPU. In: Proceedings of the Fourth International Conference on Image and Graphics, 2007.

License

This original work is copyright by University of Bremen.
Any software of this work is covered by the European Union Public Licence v1.2. To view a copy of this license, visit eur-lex.europa.eu.
The Thesis provided above (as PDF file) is licensed under Attribution-NonCommercial-NoDerivatives 4.0 International.
Any other assets (3D models, movies, documents, etc.) are covered by the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. To view a copy of this license, visit creativecommons.org.
If you use any of the assets or software to produce a publication, then you must give credit and put a reference in your publication.
If you would like to use our software in proprietary software, you can obtain an exception from the above license (aka. dual licensing). Please contact zach at cs.uni-bremen dot de.