Copyright © 2002-12-16a
In video, computer graphics, and image processing, the gamma symbol
represents a numerical parameter that describes the nonlinear
relationship between pixel value and luminance (or what you might loosely
call "intensity"). Having a good understanding of the theory
and practice of gamma will enable you to get good results when you create,
process and display pictures.
This document is available on the Internet: http:// www.poynton.com/notes/colour_and_gamma/
A typeset-quality version of this document is available: (Acrobat PDF format).
I retain copyright to this note. You have permission to use it, but you may not publish it.
Table of Contents
In a grayscale image, each pixel value represents what is loosely called brightness. However, brightness is defined formally as the attribute of a visual sensation according to which an area appears to emit more or less light. This definition is obviously subjective, so brightness is an inappropriate description of, or metric for, image data.
Grayscale image data is normally based upon luminance. Color image data is normally based upon tristimulus values. Usually, image data is coded nonlinearly: luminance, or tristimulus values, are subject to a nonlinear transfer function that mimics the lightness perception of human vision.
To understand why luminance or tristimulus values are the basis for pixel values, you must have some familiarity with these terms: radiant intensity, radiance, luminous intensity, luminance, and lightness. If you are familiar with these terms, proceed to What is gamma?
Radiant intensity refers to radiant power (flux) in a particular, specified direction. Formally, it is the rate at which radiant energy is transferred, per unit solid angle. Radiant intensity is expressed in watts per steradian (W · sr-1). It is what I call a linear-light measure.
Radiant intensity potentially has a large spatial extent, but imaging systems use pixels with small area: It is inappropriate to use intensity as a metric for image data. A more suitable quantity is radiance, defined as radiant intensity per unit projected area. It is expressed in watts per steradian per meter squared. Image data stored in a file - such as TIFF or PPM - may be proportional to radiance; however, as I have mentioned, pixel values are usually subject to a nonlinear transfer function.
In physics, radiant intensity and radiance are integrated across a wide range of wavelengths. In color science, we are interested in power only in the visible band. Radiant intensity, weighted by the spectral sensitivity associated with the brightness sensation of vision, is luminous intensity. It is expressed in units of candelas (cd). The weighting curve is defined numerically and standardized by the CIE; it is called the luminous efficiency of the Standard Observer. It is all-positive, and peaks at about 555 nm.
Luminance is luminous intensity per unit projected area. It is expressed in candelas per meter squared (cd · m-2).
Luminance, denoted Y, is proportional to power; in that sense it resembles intensity. However, its spectral composition is intimately related to the lightness sensitivity of human vision. To learn about the relationship between physical spectra and perceived brightness, and other color issues, refer to the companion Frequently Asked Questions about Color.
Strictly speaking, luminance should be expressed in units such as candelas per meter squared. In practice, luminance is often normalized to 1 or 100 units with respect to the luminance of a specified or implied white reference. For example, a studio broadcast monitor has a white reference whose luminance is about 100 cd · m-2, and Y= 1 refers to this value. So in image science, luminance is more properly called relative luminance. (A different quantity, luma, is often carelessly referred to as luminance, as I will explain below under the question What is luma?)
Luminance can be computed as a properly-weighted sum of linear-light red, green, and blue primary components - technically, tristimulus components. For contemporary video cameras, the coefficients are these:
Human vision has a nonlinear perceptual response to luminance: A source having a luminance only 18% of a reference luminance appears about half as bright. The perceptual response to luminance is called lightness, and is defined by the CIE Publication CIE No 15.2, Colorimetry, as a modified cube root of luminance:
Yn is the luminance of the white reference. If you normalize luminance to reference white then you need not compute the quotient.
Although the exponent 1/3 appears in the equation, owing to the offset and the scale factor, the overall curve is close to a 0.4-power function.
The CIE definition applies a linear segment with a slope of 903.3 near black, for (Yn) < 0.008856. The linear segment is unimportant for practical purposes but if you don't use it, make sure that you limit L* at zero. L* has a range of 0 to 100, and a delta L-star of unity is taken to be roughly the threshold of visibility.
Stated differently, lightness perception is roughly logarithmic. You cannot detect a luminance difference between two patches when the ratio of their luminance values differs by less than about one percent.
Video systems approximate the lightness response of vision using R'G'B' signals that are each subject to approximately a 0.5-power function. This is comparable to the 1/3-power function defined by L*.
Value, not to be confused withtristimulus value, refers to measures of lightness apart from CIE L*; for example, Munsell Value. Imaging systems rarely, if ever, use Value in any sense consistent with accurate color.
Video systems approximate the lightness response of vision by computing a luma component Y' as a weighted sum of nonlinear R'G'B' primary components: Each RGB signal is subject to a square root function, comparable to the 0.4-power function defined by L*. Luma is often carelessly referred to as luminance. For more information, consult the companion document Frequently Asked Questions about Color.
The luminance generated by a physical device is generally not a linear function of the applied signal. A conventional CRT has a power-law response to voltage: luminance produced at the face of the display is approximately proportional to the applied voltage raised to the 2.5 power. The numerical value of the exponent of this power function is colloquially known as gamma. This nonlinearity must be compensated in order to achieve correct reproduction of luminance.
As mentioned above (What is lightness?), human vision has a nonuniform perceptual response to luminance. If luminance is to be coded into a small number of steps, say 256, then in order for the most effective perceptual use to be made of the available codes, the codes must be assigned to luminance levels according to the properties of perception.
Here is a graph of an actual CRT's transfer function, at three different settings of the picture control:
This graph indicates a video signal having a voltage from zero to 700 mV. In a typical eight-bit digital-to-analog converter on a framebuffer card, black is at code zero, and white is at code 255.
Through an amazing coincidence, vision's response to luminance is effectively the inverse of a CRT's nonlinearity. If you apply a transfer function to code a signal to take advantage of the properties of lightness perception - a function similar to the L* function - the coding will be inverted by a CRT. For details on measuring gamma, see Roberts.
In a video system, luminance of each of the linear-light red, green, and blue (tristimulus) components is transformed to a nonlinear video signal by gamma correction, which is universally done at the camera. The Rec. 709 transfer function takes linear-light tristimulus value (here L) to a nonlinear component (here E'), for example, voltage in a video system:
The linear segment near black minimizes the effect of sensor noise in practical cameras and scanners. Here is a graph of the Rec. 709 transfer function, for a signal range from zero to unity:
An idealized monitor inverts the transform:
Real monitors are not as exact as this equation suggests, and have no linear segment, but the precise definition is necessary for accurate intermediate processing in the linear-light domain. In a color system, an identical transfer function is applied to each of the three tristimulus (linear-light) RGB components. See Frequently Asked Questions about Color.
Incidentally, the nonlinearity of a CRT is a function of the electrostatics of the cathode and the grid of an electron gun; it has nothing to do with the phosphor. Also, the nonlinearity is a power function [which has the form f (x) = xa], not an exponential function [which has the form f (x) = ex]. For more detail, read the Gamma chapter in Poynton's book Charles Poynton, A Technical Introduction to Digital Video. Chapter 6, "Gamma" is available online at (Acrobat PDF format, nnn bytes)..
Television is usually viewed in a dim environment. If an images's correct physical luminance is reproduced in a dim surround, a subjective effect called simultaneous contrast causes the reproduced image to appear lacking in contrast, as demonstrated above. The effect can be overcome by applying an end-to-end power function whose exponent is about 1.1 or 1.2. Rather than having each receiver provide this correction, the assumed 2.5-power at the CRT is under-corrected at the camera by using an exponent of about 1/2.2 instead of 1/2.5. The assumption of a dim viewing environment is built into video coding.
Standards for 625/50 systems mention an exponent of 2.8 at the decoder, however this value is unrealistically high to be used in practice. If an exponent different from 0.45 is chosen for a power function with a linear segment near black like Rec. 709, the other parameters need to be changed to maintain function and tangent continuity.
If an image originates in linear-light form, gamma correction needs to be applied exactly once. If gamma correction is not applied and linear-light image data is applied to a CRT, the midtones will be reproduced too dark. If gamma correction is applied twice, the midtones will be too light.
Viewing environments typical of computing are quite bright. When an image is coded according to video standards it implicitly carries the assumption of a dim surround. If it is displayed without correction in a bright ambient, it will appear contrasty. In this circumstance you should apply a power function with an exponent of about 1/1.1 or 1/1.2 to correct for your bright surround.
Ambient lighting is rarely taken into account in the exchange of computer images. If an image is created in a dark environment and transmitted to a viewer in a bright environment, the recipient will find it to have excessive contrast.
If an image originated in a bright environment and viewed in a bright environment, it will need no modification no matter what coding is applied. But then it will carry an assumption of a bright surround. Video standards are widespread and well optimized for vision, so it makes sense to code with a power function of 0.45 and retain a single standard for the assumed viewing environment.
In the long term, for everyone to get the best results in image interchange among applications, an image originator should remove the effect of his ambient environment when he transmits an image. The recipient of an image should insert a transfer function appropriate for his viewing environment. In the short term, you should include with your image data tags that specify the parameters that you used to encode. TIFF 6.0 has provisions for this data. You can correct for your own viewing environment as appropriate, but until image interchange standards incorporate viewing conditions, you will also have to compensate for the originator's viewing conditions.
Contrast ratio is the ratio of luminance between the brightest white and the darkest black of a particular device or a particular environment. Projected cinema film, or a photographic reflection print, has a contrast ratio of about 80:1. Television assumes a contrast ratio, in your living room, of about 30:1. Typical office viewing conditions restrict the contrast ratio of a CRT display to about 5:1.
At a particular level of adaptation, human vision responds to about a hundred-to-one contrast ratio of luminance from white to black. Call these luminance values 100 and 1. Within this range, vision can detect that two luminance values are different if the ratio between them exceeds about 1.01, corresponding to a contrast sensitivity of one percent.
To shade smoothly over this range, so as to produce no perceptible steps, at the black end of the scale it is necessary to have coding that represents different luminance levels 1.00, 1.01, 1.02, and so on. If linear light coding is used, the "delta" of 0.01 must be maintained all the way up the scale to white. This requires about 9,900 codes, or about fourteen bits per component.
If you use nonlinear coding, then the 1.01 "delta" required at the black end of the scale applies as a ratio, not an absolute increment, and progresses like compound interest up to white. This results in about 460 codes, or about nine bits per component. Eight bits, nonlinearly coded according to Rec. 709, is sufficient for broadcast-quality digital television at a contrast ratio of about 50:1.
If poor viewing conditions or poor display quality restrict the contrast ratio of the display, then fewer bits can be employed.
If a linear light system is quantized to a small number of bits, with black at code zero, then the ability of human vision to discern a 1.01 ratio between adjacent luminance levels takes effect below code 100. If a linear light system has only eight bits, then the top end of the scale is only 255, and contouring in dark areas will be perceptible even in very poor viewing conditions.
As outlined above, gamma correction in video effectively codes into a perceptually uniform domain. In video, a 0.45-power function is applied at the camera, as shown in the top row of this diagram:
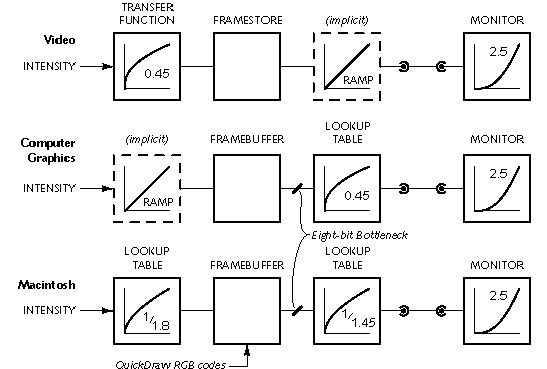
Synthetic computer graphics calculates the interaction of light and objects. These interactions are in the physical domain, and must be calculated in linear-light values. It is conventional in computer graphics to store linear-light values in the framebuffer, and introduce gamma correction at the lookup table at the output of the framebuffer. This is illustrated in the second row.
If linear-light is represented in just eight bits, near black the steps between codes will be perceptible as banding in smoothly-shaded images. This is the eight-bit bottleneck in the sketch.
Desktop computers are optimized neither for image synthesis nor for video. They have programmable "gamma" and either poor standards or no standards. Consequently, image interchange among desktop computers is fraught with difficulty.
In a pseudocolor (or indexed color) framebuffer, each pixel value in the frame buffer (e.g., 43) is presented to the color lookup table (CLUT); the CLUT returns an RGB triple (e.g., 135, 206, 235). Each mapped value, plus or minus a black-level error, is proportional to voltage.
In a hicolor framebuffer (for 16-bit color, on a cheap-o PC), with five bits for each of red, green, and blue, each component (0 to 31), plus or minus a black-level error, is proportional to voltage.
In a truecolor framebuffer, each of the three 8-bit components is mapped through one of three lookup tables (LUTs, one for each of red, green, and blue) to produce a code from 0 to 255. Each lookup table can impose an arbitrary transfer function. The mapping may be determined by application software or system software; it may or may not be accessible to the user, and may be well documented, poorly documented, or undocumented. Each mapped value, plus or minus a black-level error, is proportional to voltage.
the companion Frequently Asked Questions about Color for more information about colormapped, hicolor, and truecolor systems.
Apple offers no definition of the nonlinearity - or loosely speaking, gamma - that is intrinsic in QuickDraw. But the combination of a default QuickDraw lookup table and a standard monitor causes luminance to represent the 1.8-power of the R, G, and B values presented to QuickDraw. It is wrongly believed that Macintosh computers use monitors whose transfer function is different from the rest of the industry. The unconventional QuickDraw handling of nonlinearity is the root of this misconception. Macintosh coding is shown in the bottom row of the diagram. More detail is available in Poynton's article Gamma on the Apple Macintosh available on the Internet (Acrobat PDF format, nnn bytes).
The transfer of image data in computing involves various transfer functions: at coding, in the framebuffer, at the lookup table, and at the monitor. Strictly speaking the term gamma applies to the exponent of the power function at the monitor. If you use the term loosely, in the case of a Mac you could call the gamma 1.4, 1.8 or 2.5 depending which part of the system you were discussing.
I recommend using the Rec. 709 transfer function, with its 0.45-power law, for best perceptual performance and maximum ease of interchange with digital video. If you need Mac compatibility you will have to code luminance with a 1/1.8-power law, anticipating QuickDraw's 1/1.45-power in the lookup table. This coding has adequate performance in the bright viewing environments typical of desktop applications, but suffers in darker viewing conditions that have high contrast ratio.
Gamma of a properly adjusted conventional CRT varies anywhere between about 2.35 and 2.55.
CRTs have acquired a reputation for wild variation for two reasons.
First, if the model
luminance = voltage is naively
fitted to a display with black-level error, the exponent deduced will
be as much a function of the black error as the true exponent. Second,
input devices, graphics libraries, and application programs all have the
potential to introduce their own transfer functions. Nonlinearities from
these sources are often categorized as gamma and wrongly attributed to the
display.
On a CRT monitor, the picture control, often misleadingly labelled contrast, adjusts overall luminance. The black level control, often misleadingly labelled brightness, adjusts offset. Display a picture that is predominantly black. Adjust black level so that the monitor reproduces true black on the screen, just at the threshold where it is not so far down as to "swallow" codes greater than the black code, but not so high that the picture sits on a pedestal of dark grey. When the critical point is reached, put a piece of tape over the black level control. Then set picture to suit your preference for display luminance.
If you wish to simulate the physical world, linear-light coding is necessary. For example, if you want to produce a numerical simulation of a lens performing a Fourier transform, you should use linear coding. If you want to compare your model with the transformed image captured from a real lens by a video camera, you will have to "remove" the nonlinear gamma correction that was imposed by the camera, to convert the image data back into its linear-light representation.
On the other hand, if your computation involves human perception, a nonlinear representation may be required. For example, if you perform a discrete cosine transform on image data as the first step in image compression, as in JPEG, then you ought to use nonlinear coding that exhibits perceptual uniformity, because you wish to minimize the perceptibility of the errors that will be introduced during quantization.
The image processing literature rarely discriminates between linear and nonlinear coding. In the JPEG and MPEG standards there is no mention of transfer function, but nonlinear (video-like) coding is implicit: unacceptable results are obtained when JPEG or MPEG are applied to linear-light data. In computer graphic standards such as PHIGS and CGM there is no mention of transfer function, but linear-light coding is implicit. These discrepancies make it very difficult to exchange image data between systems.
When you ask a video engineer if his system is linear, he will say Of course! - referring to linear voltage. If you ask an optical engineer if her system is linear, she will say Of course! - referring to linear luminance. But when a nonlinear transform lies between the two systems, as in video, a linear transformation performed in one domain is not linear in the other.
To conform with the definition of luminance as being proportional to physical power, the I component of HSI should represent a linear-light quantity. The CIE has defined no objective measure for brightness, but it is clearly a perceptual quantity. Lightness is a perceptual quantity that has been quite precisely defined by the CIE. The CIE has not defined Value, but several different definitions are in use, such as Munsell Value, and all have a perceptual basis and are comparable to lightness.
In most formulations of HSI, HSB, HLS, and HSV used in computer graphics, the quantities are computed from R, G, and B primary components but no reference is made to the nonlinearity in the primary components, that is, the relationship of the primaries to linear light. So it is impossible to determine whether the calculated HSI, HSB, HLS, or HSV represents a physical or a perceptual quantity.
The brightness component of HSI, HSB, HLS, and HSV should be based on luminance, computed as a properly-weighted sum of red, green, and blue. But in the usual formulations, the brightness component is computed as either the maximum of the three components, or the average of the minimum and the maximum of the three. This highly nonlinear calculation introduces spokes into the hue circle.
Finally, the color produced by an RGB triple translated from HSI, HSB, HLS, or HSV depends on the chromaticity of the RGB primaries, but none of the usual formulations of HSI, HSB, HLS, or HSV takes primary chromaticity into account.
For these reasons, any use in computer graphics of I, B, L, and V quantities is suspect. For detail, see Frequently Asked Questions about Color.
A image destined for halftone printing conventionally specifies each pixel in terms of dot percentage in film. An imagesetter's halftoning machinery generates dots whose areas are proportional to the requested coverage. In principle, dot percentage in film is inversely proportional to linear-light reflectance.
Two phenomena distort the requested dot coverage values. First, printing involves a mechanical smearing of the ink that causes dots to enlarge. Second, optical effects within the bulk of the paper cause more light to be absorbed than would be expected from the surface coverage of the dot alone. These phenomena are collected under the term dot gain, which is the percentage by which the light absorption of the printed dots exceeds the requested dot coverage.
Standard offset printing involves a dot gain at 50% of about 24%: when 50% absorption is requested, 74% absorption is obtained. The midtones print darker than requested. This results in a transfer function from code to reflectance that closely resembles the voltage-to-light curve of a CRT. Correction of dot gain is conceptually similar to gamma correction in video: physical correction of the "defect" in the reproduction process is very well matched to the lightness perception of human vision. Coding an image in terms of dot percentage in film involves coding into a roughly perceptually uniform space. The standard dot gain functions employed in North America and Europe correspond to luminance being reproduced as a power function of the digital code, where the numerical value of the exponent is about 1.75, compared to about 2.2 for video. This is lower than the optimum for perception, but works well for the low contrast ratio of offset printing.
The Macintosh has a power function that is close enough to printing practice that raw QuickDraw codes sent to an imagesetter produce acceptable results. High-end publishing software allows the user to specify the parameters of dot gain compensation.
I have described the linearity of conventional offset printing. Other halftoned devices have different characteristics, and require different corrections.
),"
in EBU Technical Review 257 (Autumn 1993), 32-40.